Элементы алгебры логики

 

 

Алгебра - наука об общих операциях, аналогичных  сложению и умножению, которые могут выполняться над разнообразными математическими объектами – числами, многочленами, векторами и др. Логика – это наука о формах и способах мышления. Алгебра логики  - раздел математической логики, в котором изучаются логические операции над высказываниями. 

 

Высказывание - это основной элемент логики, определяемый как повествовательное предложение, относительно которого можно однозначно сказать, истинное или ложное утверждение оно содержит. Вопросительное, побудительное и восклицательное предложения не являются высказываниями, так как в них ничего не утверждается и не отрицается.

 

Высказывания бывают простыми и сложными. Высказывание называется простым (элементарным), если никакая его часть сама не является высказыванием.

Примеры простых высказываний: Листва на деревьях опадает осенью. Земля прямоугольная. Первое высказывание содержит истинную информацию, а второе - ложную.

Высказывания могут быть и такими: 2>1, Н2О+SO3=H2SO4. Здесь используются языки математических символов и химических формул.

Из простых высказываний можно получить сложные, объединив их с помощью логических связок. Логические связки (операции) - слова, которые подразумевают определённые логические связи между высказываниями. В математической логике это “и”, “или”, “не”, “если ... то”, “либо ... либо” и другие. Таким образом, сложные (составные) высказывания строятся из простых с помощью логических операций.

Кроме того, высказывания бывают общими, частными и единичными. Общее высказывание начинается со слов: всё, все, всякий, каждый, ни один. Частное высказывание начинается со слов: некоторые, большинство и т.п. Во всех других случаях высказывание является единичным.

 

Алгебра логики подразумевает, что каждая переменная может принимать только два значения: истинно или ложно. Для обозначения переменных принимают символы 0 и 1, которые по написанию совпадают с обычными арифметическими единицей и нулём. Совпадение это только внешнее, так как смысл они имеют совсем иной. Логическая 1 означает, что какое-то событие истинно, а логический 0 означает, что высказывание не соответствует истине, то есть  ложно.

Высказывание заменяется на логическое выражение, которое строится из логических переменных (А, В, Х, …) и логических операций (связок).

    В алгебре логики знаки операций обозначают лишь три логические связки ИЛИ, И, НЕ. 

 

Составные высказывания в алгебре логики записываются с помощью логических выражений. Для любого логического выражения достаточно просто построить таблицу истинности. Таблицу, показывающую, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний, называют таблицей истинности логического высказывания.

В левой части этой таблицы перечисляются все возможные значения аргументов функции (то есть входные величины), а в правой указывается соответствующее им значение логической функции. 

 

1.     Для логической операции ИЛИ таблица истинности имеет вид:

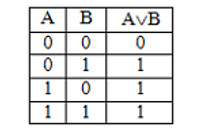
Операцию ИЛИ называют также логическим сложением, и потому её можно обозначать знаком «+». Другое обозначение: АvВ

Рассмотрим сложное единичное высказывание: «Летом я поеду в деревню или в туристическую поездку». Обозначим через А простое высказывание «Летом я поеду в деревню», а через В - простое высказывание «Летом я поеду в туристическую поездку». Тогда логическое выражение сложного высказывания имеет вид А+В, и оно будет ложным только, если ни одно из простых высказываний не будет истинным.

 

2.  Для логической операции И таблица истинности имеет вид:

Из таблицы истинности следует, что операция И - это логическое умножение, которое ничем не отличается от умножения в обычной алгебре. Операцию И можно обозначить знаком по-разному:

В формальной логике операции логического умножения соответствуют связкам «и», «а», «но», «хотя».

 

3. Логическая операция НЕ -  эта операция является специфичной для алгебры логики и не имеет аналога в обычной алгебре. Она обозначается чертой над значением переменной, либо знаком приставки перед значением переменной: 

 

Читается в обоих случаях одинаково «Не А». Таблица истинности для этой функции имеет вид: 

Данная операция соответствует в формальной логике связкам «не»; «неверно, что».

 

В вычислительной технике операцию НЕ называют отрицанием или инверсией, операцию ИЛИ - дизъюнкцией, операцию И - конъюнкцией.

 

Логические операции имеют следующий приоритет: действия в скобках, инверсия, & (конъюнкция), v (дизъюнкция).

 

Алгоритм построения таблицы истинности:

 

1. подсчитать количество переменных n в логическом выражении;

2. подсчитать количество логических операций в выражении;

3. установить последовательность выполнения логических операций с учётом скобок и приоритетов;

4. определить количество столбцов в таблице: число переменных плюс число операций;

5. заполнить шапку таблицы, включив в неё переменные и операции;

6. определить число строк в таблице (без шапки) m = 2ⁿ;

7. выписать наборы входных переменных с учётом того, что они представляют собой натуральный ряд n-разрядных двоичных чисел от 0 до 2ⁿ-1; 

8. провести заполнение таблицы по столбцам, выполняя логические операции в соответствии с установленной последовательностью.

Наборы входных переменных, во избежание ошибок, рекомендуют перечислять следующим образом:

а) определить количество наборов входных переменных;

б) разделить колонку значений первой переменной пополам и заполнить верхнюю часть колонки 0, а нижнюю - 1;

в) разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами 0 или 1, начиная с группы 0;

г) продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами 0 или 1 до тех пор, пока группы 0 и 1 не будут состоять из одного символа.